Thursday, October 21, 2010
Wednesday, October 20, 2010
angle bisector construction
angle bisector constrution
Monday, October 18, 2010
Wednesday, October 13, 2010
angles classwork
angle bisector
Step 1 : Put the sharp end of your compasses at point B and make one arc on the line BC (point S) and another arc on line AB (point T).
Step 2 : Without changing the width of your compasses, put the sharp end of the compasses at S and make an arc within the lines AB and BC. Do the same at T and make sure that the second arc intersects the first arc
Step 3 : Draw a line from point B to the points of intersection of the 2 arcs. This line bisects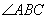 .
.
perpendicular bisetor
Step 1 : Stretch your compasses until it is more then half the length of AB. Put the sharp end at A and mark an arc above and another arc below line segment AB.
Step 2 : Without changing the width of the compasses, put the sharp end at B and mark arcs above and below the line segment AB that will intersect with the arcs drawn in step
Step 3 : Join the two points where the arcs intersect with a straight line. This line is the perpendicular bisector of AB. P is the midpoint of AB.
median
Constructing a median with a compass
Open the compass past the estimated midpoint of the side. Strike an arc. Keeping the same setting, move to the vertex on the opposite side of the side you are working with. Strike an arc such that it intersects the first arc twice. Use a straightedge to find the midpoint of the side. Draw a segment from that midpoint to the opposite vertex. Do this for all three sides and you'll find the centroid of the
altitude
1. If the apex of the triangle is not over the base (one of the base angles is obtuse), then extend the base line so that it goes beyond the point where the altitude would intersect.
2. Set a compass to a distance slightly larger than the altitude. Keep it at this setting for the next step of the construction.
3. With the point of the compass on the triangle's apex, mark the base line (and/or its extension) at the two points whose distance from the apex matches the compass/divider setting.
4. Set the compass to a distance larger than the distance between the points just marked. (Its former setting will do; you don't have to change it.) Keep this setting throughout the next step.
5. With the point of the compass on one of the marked points on the baseline, draw an arc below the baseline across the space between the marked baseline points. Do the same with the point of the compass on the other marked baseline point.
6. Using a straightedge, line up the apex of the triangle and the intersection point of the arcs just drawn. The altitude of the triangle is the line segment along the straightedge that extends from the apex to the baseline
mid segment
If 3 parallel lines form congruent segments along one transversal, then they form congruent segments along every transversal. If a line intersects the midpoint of one side a triangle and is parallel to another side of the triangle, then it intersects the midpoint of the third side of the triangle. If a segment joins the midpoints of two sides of a triangle, then the segment is (a) parallel to the third side of the triangle, and (b) half the length of the third
Step 1 : Put the sharp end of your compasses at point B and make one arc on the line BC (point S) and another arc on line AB (point T).
Step 2 : Without changing the width of your compasses, put the sharp end of the compasses at S and make an arc within the lines AB and BC. Do the same at T and make sure that the second arc intersects the first arc
Step 3 : Draw a line from point B to the points of intersection of the 2 arcs. This line bisects
perpendicular bisetor
Step 1 : Stretch your compasses until it is more then half the length of AB. Put the sharp end at A and mark an arc above and another arc below line segment AB.
Step 2 : Without changing the width of the compasses, put the sharp end at B and mark arcs above and below the line segment AB that will intersect with the arcs drawn in step
Step 3 : Join the two points where the arcs intersect with a straight line. This line is the perpendicular bisector of AB. P is the midpoint of AB.
median
Constructing a median with a compass
Open the compass past the estimated midpoint of the side. Strike an arc. Keeping the same setting, move to the vertex on the opposite side of the side you are working with. Strike an arc such that it intersects the first arc twice. Use a straightedge to find the midpoint of the side. Draw a segment from that midpoint to the opposite vertex. Do this for all three sides and you'll find the centroid of the
altitude
1. If the apex of the triangle is not over the base (one of the base angles is obtuse), then extend the base line so that it goes beyond the point where the altitude would intersect.
2. Set a compass to a distance slightly larger than the altitude. Keep it at this setting for the next step of the construction.
3. With the point of the compass on the triangle's apex, mark the base line (and/or its extension) at the two points whose distance from the apex matches the compass/divider setting.
4. Set the compass to a distance larger than the distance between the points just marked. (Its former setting will do; you don't have to change it.) Keep this setting throughout the next step.
5. With the point of the compass on one of the marked points on the baseline, draw an arc below the baseline across the space between the marked baseline points. Do the same with the point of the compass on the other marked baseline point.
6. Using a straightedge, line up the apex of the triangle and the intersection point of the arcs just drawn. The altitude of the triangle is the line segment along the straightedge that extends from the apex to the baseline
mid segment
If 3 parallel lines form congruent segments along one transversal, then they form congruent segments along every transversal. If a line intersects the midpoint of one side a triangle and is parallel to another side of the triangle, then it intersects the midpoint of the third side of the triangle. If a segment joins the midpoints of two sides of a triangle, then the segment is (a) parallel to the third side of the triangle, and (b) half the length of the third
Subscribe to:
Posts (Atom)




